Tứ giác nội tiếp, đa giác đều và phép quay
Bài tập Cơ bản:
Câu 1: Sắp xếp các câu để được bài chứng minh
Cho đường tròn đường kính AB và D là một điểm thuộc đường tròn ( D khác A và B). Trên tia đối của tia BA lấy một điểm C. Đường thẳng vuông góc với BC tại C cắt đường thẳng AD tại M. Chứng minh tứ giác MCBD nội tiếp.
Câu 2: Sắp xếp các câu để được bài chứng minh
Cho tam giác ABC nội tiếp đường tròn (O) đường kính AB. Đường thẳng vuông góc với AO tại trung điểm I của AO cắt AC tại M và cắt tiếp tuyến tại C của đường tròn tại E. Chứng minh tứ giác OCEI nội tiếp.
Tứ giác OCEI nội tiếp đường tròn (dấu hiệu nhận biết)
Ta có: OCE = 90 độ (tính chất tiếp tuyến)
EIO = 90 độ (giả thiết)
OCE + EIO = 90 độ + 90 độ = 180 độ
Khẳng định nào sau đây không đúng?
Một tứ giác nội tiếp được nếu:
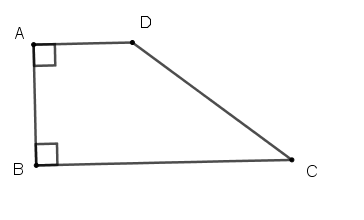
Câu 7: Điền số thích hợp vào chỗ trống
Đáp số:
Câu 8: Sắp xếp các câu để được bài chứng minh
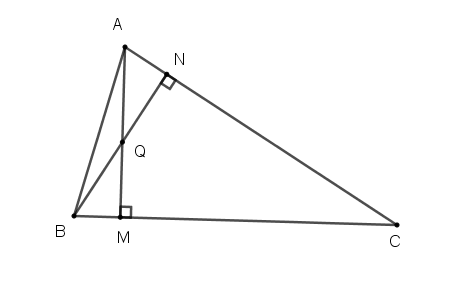
Cho tam giác nhọn ABC, đường cao AD. Gọi AM,AN là các tiếp tuyến với đường tròn (O) đường kính BC (M,N là các tiếp điểm). Chứng minh AMDN là tứ giác nội tiếp.
Hướng dẫn giải (chi tiết)
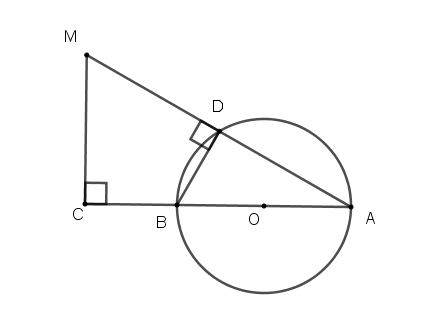
Ta có: (giả thiết)
(góc nội tiếp chắn nửa đường tròn)
(kề bù với )
Tứ giác nội tiếp đường tròn (dấu hiệu nhận biết)
Câu 2: Sắp xếp các câu để được bài chứng minh
Hướng dẫn giải (chi tiết)
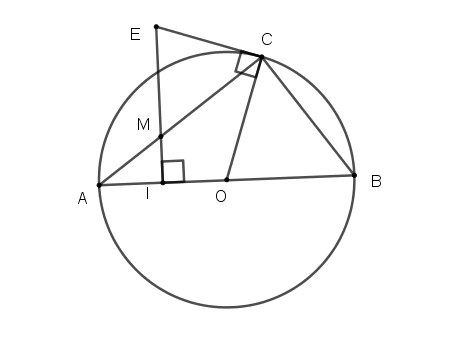
Ta có: (tính chất tiếp tuyến)
(giả thiết)
Tứ giác nội tiếp đường tròn (dấu hiệu nhận biết)
Hướng dẫn giải (chi tiết)
Hình chữ nhật là hình có bốn đỉnh cách đều giao điểm của hai đường chéo nên luôn nội tiếp được trong một đường trònCác hình còn lại không đúng
Vậy đáp án là D
D. Bốn điểm nằm trên một đường tròn
Hướng dẫn giải (chi tiết)
Ta có: (giả thiết)Tứ giác nội tiếp đường tròn (dấu hiệu nhận biết)
Hay bốn điểm nằm trên một đường tròn và bốn điểm nằm trên một đường tròn
Tam giác vuông tại nên tâm đường tròn ngoại tiếp tam giác là trung điểm đoạn
Do ba điểm thẳng hàng nên không tồn tại đường tròn đi qua ba điểm trên
Suy ra khẳng định A, B, C đúng, khẳng định D sai.
Vậy đáp án là D
C. Tứ giác có tổng hai góc bằng
Hướng dẫn giải (chi tiết)
Dấu hiệu nhận biết tứ giác nội tiếp là:1. Tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện
2. Tứ giác có tổng hai góc đối diện bằng
3. Tứ giác có hai đỉnh cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc
4. Tứ giác có bốn đỉnh cách đều một điểm
Vậy khẳng định không đúng là C
Vậy đáp án là C
Câu 6: Hãy chọn đáp án đúng
Đáp án đúng là:
D. 
Hướng dẫn giải (chi tiết)
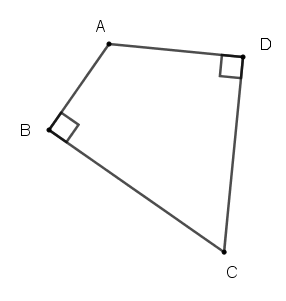
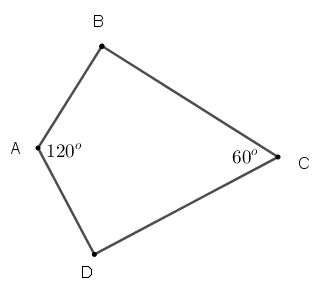
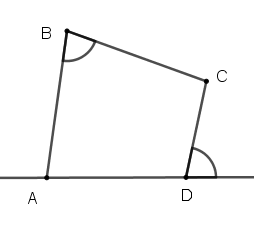
Đáp án A và B có tổng hai góc đối nhau bằng nên nội tiếp đường trònĐáp án C có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện nên nội tiếp trong đường tròn
Suy ra hình D không phải là tứ giác nội tiếp trong đường tròn
Vậy đáp án là D
Câu 7: Điền số thích hợp vào chỗ trống
Hướng dẫn giải (chi tiết)
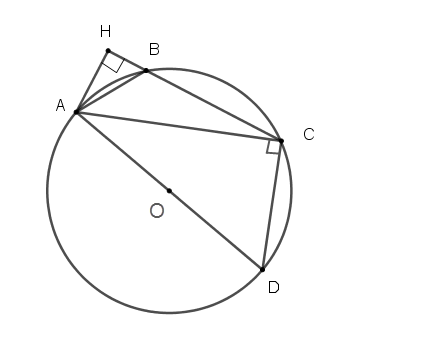
Kẻ đường kính của
(góc nội tiếp chắn nửa đường tròn)
Ta có nội tiếp đường tròn
(góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện)
Xét và có:
(g.g)
(tỉ số đồng dạng)
Vậy số cần điền là
Hướng dẫn giải (chi tiết)
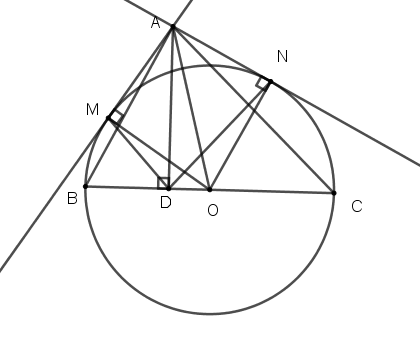
Ta có: (tính chất tiếp tuyến)
(giả thiết)
Các điểm cùng nhìn cạnh dưới góc
Các điểm cùng thuộc một đường tròn (dấu hiệu nhận biết)
là tứ giác nội tiếp
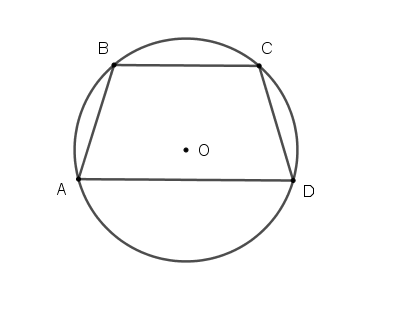
Ta có nội tiếp đường tròn
(tổng hai góc đối diện) (1)
Do (tổng hai góc trong cùng phía) (2)
Từ (1) và (2)
là hình thang cân
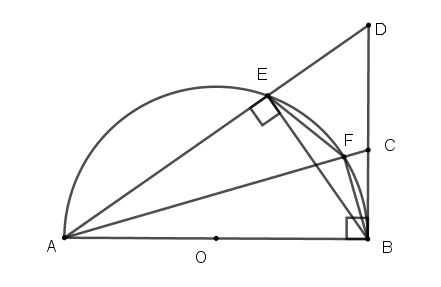
Ta có: (góc nội tiếp chắn nửa đường tròn);
(tính chất tiếp tuyến)
(cùng phụ với )
Mặt khác (hai góc nội tiếp cùng chắn một cung)
là tứ giác nội tiếp (dấu hiệu nhận biết)



